Proposal for Swarm DISC ITT 1.1
Multi-approach gravity �eld models
from Swarm GPS data
Although the knowledge of the gravity of the Earth has improved considerably with the CHallenging Mini-Satellite Payload (CHAMP) (Reigber2002; Reigber, Schwintzer and Luehr 1996), Gravity Recovery And Climate Experiment (GRACE) (Tapley, Reigber and Melbourne 1996; Tapley et al. 2004) and Gravity �eld and steady-state Ocean Circulation Explorer (GOCE) (Balmino et al. 1999; Floberghagen et al. 2011) satellite missions, the geophysical community has identi�ed the need for the continued monitoring of its time-variable component with the purpose of estimating the hydrological and glaciological yearly cycles and long-term trends. Currently, the GRACE satellites are the sole provider of this data and the GRACE Follow On (GRACE-FO) (Sheard et al. 2012; Larkin 2012; Flechtner et al. 2014) mission aims to take over this role after December 2017. The current proposal aims at providing the high-quality gravity �eld models from Swarm data that constitute an alternative source of gravimetric data, which could help alleviate the consequences of the potential gap between GRACE and GRACE-FO, as well as the short gaps in the existing GRACE data. Independently on the existence of gravimetric data from dedicated satellite missions, the gravity �eld models derived from Swarm GPS data constitute an independent source of information about Earth's gravity �eld, e.g. for monitoring large mass transport processes (Teixeira Encarnação et al., 2017).
Recently, the geodetic community has realised that the combination of the di�erent gravity �eld solutions is superior to any individual model, as demonstrated for GRACE by Jean, Meyer and Jäggi (2015a) and Jean, Meyer and Jäggi (2015b), and for Swarm by Teixeira da Encarnação et al. (2016). In response to the call for Swarm gravity �eld models issue by the Data, Innovation and Science Cluster (DISC) consortium, we intend to exploit of this fact and deliver to highest quality gravity �eld models, resulting from the combination of 4 di�erent gravity �eld estimation approaches.
Additionally, we intend to evaluate the added value of Kinematic Baselines (KBs) in the quality of the combined gravity �eld model. For that purpose, 2 di�erent KBs solutions will be studied within the context of the project. The choice of which KB solution (if any) is used for the production of the models of the various institutes is left to the respective responsible scientist. To answer the Statement of Work (SoW), we will also determine the bene�t of two di�erent models of non-gravitational forces and the measured non-gravitational accelerations from Swarm-C to the quality of the gravity �eld models.
The strong points of our proposal are i) the statistically-optimal combination of models derived with 4 di�erent gravity estimation strategies, each producing state-of-the-art Swarm gravity �eld models, ii) the use of 3 independently-developed Precise Orbit Determination (POD) software packages to estimate the Kinematic Orbits (KOs), iii) the analysis of the improvement resulting from using accelerometer measurements from Swarm-C or 2 di�erent non-gravitational force models and iv) the study of the added value to the quality of the gravity �eld models when considering the KBs computed with 2 di�erent strategies.
A prerequisite for the proposed objectives is the involvement of numerous institutions. This has the unfortunate disadvantage of diluting the funding and limiting considerably the time devoted to project activities. In spite of this, we have constructed a WP arrangement that minimizes overhead costs and maximizes independent progress, in order to fully take advantage of the available resources.
The work plan considered in this proposal is based on the tasks speci�ed in the SoW:
Each task is addressed with the following WPs:
At the end of the project the following main results are expected:
The Technical Proposal is provided in 2 of this document, in which we show our understanding of the project requirements and describe the methodology we propose to meet those requirements.
The Implementation Proposal can be found in 3, describing the WPs, their distribution amongst the study team, the schedule, the list of deliverables and the preliminary risk assessment.
4 contains the Management Proposal, where details on the study team are given, their roles in the project are presented, the organisation and management of the project is described and a few adjustments on the project requirements (Section 5 of the SoW) are proposed.
The Financial Proposal is shown in ??, where the Price Quotation is given, the sub-contracting plan is presented, the inclusion of OSU (operating from a non-ESA member state, USA) is motivated (in ??) and small modi�cation to the Payment Plan is proposed.
Finally, the Contractual Proposal is covered in ??, the price summary is present in ??, the compliance matrix is �lled and signed in ??, the Curricula Vit� (CVs) of the team members are given in ?? and the Procedures Speci�cations and Standards (PSS) A2 and A8 forms are in ??.
The electronic version of this document contains unmarked links in table (e.g. 1), �gure (e.g. 1), section (e.g. 1) and literature references (e.g. Allende-Alba et al. (2017)), as well as in acronyms (e.g. GRACE), URLs (e.g. www.aiub.unibe.ch) and WP numbers (e.g. WP100).
The Technical Proposal provides the team's interpretation of the Statement of Work. It does this by o�ering a detailed description of the technical work to be performed, and the proposed approach in taking on this work.
The GPS instruments on-board the three Earth's Magnetic Field and Environment Explorer (Swarm) satellites collects highly accurate hl-SST data (IJssel et al., 2015; IJssel, Forte and Montenbruck, 2016), with su�cient quality to measure the monthly gravity �eld model at basin-wide spatial scales (Teixeira da Encarnação et al., 2016).
We propose to produce the state-of-the-art models that are the results of the statistically-optimal combination of 4 gravity �eld models produced with di�erent gravity �eld inversion strategies. As a result, the combined model bene�ts from the strong aspects of every approach and are consistently better than any individual solution, as demonstrated for GRACE (Jean, Meyer and Jäggi, 2015b; Jean, Meyer and Jäggi, 2015a), Swarm (Teixeira da Encarnação et al., 2016). In this proposal, the term individual solution refers to the gravity �eld models produced with one of the 4 approaches described in 2.3. In contrast, the combined model refers to the result of the combination of all individual solutions.
In 1, the superior quality of the combined models is clearly illustrated by the smaller amplitude of the combined model (in dark red), relative to the individual solutions.

The combination strategy exploited to produce 1 was simple arithmetic averaging, which is sub-optimal. The proper combination of the individual models considering the error variance-covariance is expected to increase the quality of the combined model.
To answer Task 2 of the SoW, the analysis of 3 di�erent types of non-gravitational accelerations will be conducted. Two models are going to be considered (one implemented by TU Delft and the other by ASU) as well as the accelerometer measurements collected by Swarm-C.
Modelled non-gravitational accelerations produced at TU Delft
Modelled non-gravitational acceleration time series for all three Swarm satellites are
already routinely produced at TU Delft as part of the Swarm ESL Level 2 (L2) processing
activities (Siemes2016). These time series are available as an intermediate L2 product
(ACCx_FMi2). Currently, the aerodynamic forces are based on the satellite panellised
geometry speci�cation received from ESA, but an upgrade will be made to use normalised
force coe�cients obtained from the SPARTA free-molecular �ow analysis software (Gallis
et al., 2014), based on a highly detailed Computer-Aided Design (CAD) geometry
model.
The empirical thermosphere density model that is used in the Swarm L2 ACCx_FMi2 non-gravitational acceleration models (currently NRLMSISE-00) is known to contain time-variable biases related to changes in solar activity level, which deteriorates the quality of the acceleration data. Such errors can be signi�cantly reduced by replacing the solar activity input to the density model (F10.7 for NRLMSISE-00) by values estimated from the Swarm L2 DNSxPOD_2 product. If this correction is performed only for the part of the bias that changes slowly, over days and longer periods, it will eliminate the solar-activity-dependent biases in the non-gravitational acceleration time series to a very large extent, while keeping the in�uence of the gravity �eld models used in the ACCxPOD processing to a minimum.
Modelled non-gravitational accelerations produced at ASU
For processing the satellite orbital data, the coordinate transformations and the generation
of modelled forces, on which the creation of the modelled non-gravitational accelerations
of each Swarm satellite is based, the ASU home-made orbital propagator NUMINTSAT is
used (Bezděk et al., 2009). In order to compute the non-gravitational forces, ESA provides
scienti�c users with the physical properties of the satellite, its mass, cross-section in a
speci�c direction, radiation properties of the satellite's surface and a macromodel
approximately characterizing the shape of the Swarm satellites. When representing the
force due to atmospheric drag, we paid special attention to quantities usually having most
uncertainty in their speci�c values. For neutral atmospheric density, we made use of the
NRLMSISE-00 model. To have a realistic drag coe�cient, for each satellite we estimated it
by means of the long-term change in orbital elements. The details of our approach
can be found in references, e.g. (Bezděk, 2010; Bezděk et al., 2014; Bezděk et al.,
2016).
Measured non-gravitational accelerations
The measured non-gravitational accelerations produced in ASU are based mainly on the
Level 1A (L1A) product ACCxSCI_1A, which provide the observations from an
accelerometer aboard each Swarm satellite. A rather strong in�uence of temperature on
Swarm accelerometer data has been evident since the mission start; on the other hand, it
was demonstrated that the physical non-gravitational signal was also recorded, most
clearly in the along-track accelerometer component of Swarm-C (Siemes2016; Bezděk,
Sebera and Klokočník, 2014). The modelled non-gravitational accelerations look like a
smoothed version of the accelerometer observations, but the accelerometer data generally
supersede the modelled non-gravitational accelerations by providing more detailed
information on high-frequency contents of the external perturbations. Besides, the
accelerometer measurements show the spikes corresponding to activating the
satellite thrusters and other satellite-related phenomena, which are not present in
the non-gravitational models. To reduce the high temperature dependence, we
apply a method of linear temperature correction; we presented its successful
use on several Swarm Cal/Val meetings and recently in a publication (Bezděk
et al., 2016). So far, and in accordance with results presented by the ESA team
(Siemes2016), acceptable results have been obtained only for the accelerometer data in
the along-track component of Swarm-C. In this project, we will investigate the
possibility to calibrate the other two components of Swarm-C (cross-track and
radial) and their possible use for the gravity �eld inversion. Thus, the modelled
non-gravitational accelerations from ASU or TU Delft will replace the gaps in Swarm-C
accelerometer data and represent the non-gravitational accelerations in Swarm A and
B.
| Institute | Location | Software | Reference |
| AIUB | Bern, Switzerland | Bernese! (Dach2015) | Jäggi et al. (2016) |
| IfG | Graz, Austria | Gravity Recovery Object Oriented Programming System (GROOPS) (in-house development) | Zehentner and Mayer-Gürr (2016) |
| TUD | Delft, Netherlands | GPS High precision Orbit determination Software Tool (GHOST) (Helleputte 2004; Wermuth, Montenbruck and Helleputte 2010) | IJssel et al. (2015) |
Kinematic Orbits produced at TU Delft
Kinematic orbits for the Swarm satellites are routinely computed by TU Delft in the
framework of the Swarm ESL L2 processing. The detailed processing strategy that is used to
compute these orbits is described in (IJssel et al., 2015). Using independent Satellite Laser
Ranging (SLR) validation it is shown that for the �rst year of mission operations these
kinematic orbits have an accuracy of about 4-5 cm.
It is also shown that the Swarm GPS observations are noticeably a�ected by ionospheric scintillation, which leads to slightly larger kinematic orbit errors close to the geomagnetic poles and along the geomagnetic equator. Meanwhile several GPS receiver tracking loop modi�cations have been implemented to increase the receiver robustness for ionospheric scintillation (IJssel, Forte and Montenbruck, 2016). In addition, going from solar maximum conditions at the start of the mission to lower solar activity in the current solar cycle has also reduced the occurrence and intensity of ionospheric scintillation. Therefore it is expected that the recent kinematic Swarm orbits have slightly improved accuracy levels.
As kinematic orbits do not involve any a priori assumptions on the spacecraft dynamics, they are well suited for the recovery of the Earth's gravity �eld. For best performance the covariance information should also be taken into account in the gravity �eld recovery. For this project, therefore also covariance information of the kinematic orbits will be provided.
Kinematic Orbits produced at AIUB
The AIUB generates both kinematic and reduced-dynamic Low-Earth Orbit (LEO) orbits.
The method to generate these types of orbits with the Bernese GNSS software (Bernese)
(Dach2015) has been successfully used for POD of many di�erent Low-Earth Orbiters, e.g.,
CHAMP, GRACE, Jason-2, MetOp-A, GOCE, TerraSAR-X and TanDEM-X, the Swarm and the
Sentinel satellites (Jäggi, Hugentobler and Beutler, 2006; Jäggi et al., 2007; Bock et al., 2011;
Jäggi et al., 2012; Jäggi et al., 2016), and is described in detail in Jäggi, Hugentobler
and Beutler (2006). The standard orbit determination procedures are based on a
batch least-squares approach using zero-di�erence ionosphere-free GPS carrier
phase data. They were operationally used for the Precise Science Orbit (PSO)
determination in the frame of the GOCE High-Level Processing Facility (HPF) (Bock et al.,
2014) and are used for i) an independent assessment of the Swarm data in the
frame of the Swarm Quality Working Group (QWG) (Dahle, Arnold and Jäggi, 2017)
and ii) an independent validation of the o�cial Sentinel orbit products in the
frame of the Sentinel POD QWG of the Copernicus POD Service (Peter et al., 2017).
The kinematic LEO positions are purely geometrical solutions of a Precise Point
Positioning (PPP) as implemented in the Bernese! and are derived together with
epoch-wise covariance information from the GPS phase observations and attitude data
collected on-board the LEO satellites. Kinematic positions from CHAMP, GOCE, and
Swarm were used to recover the long wavelength part of the Earth's gravity �eld and
to study the capability of GPS hl-SST tracking to recover time variations of the
Earths gravity �eld (Weigelt et al., 2013; Jäggi et al., 2016; Dahle, Arnold and Jäggi,
2017).
Kinematic Orbits produced at IfG
KOs are produced at the IfG applying the in-house developed raw observation approach
(Zehentner and Mayer-Gürr, 2016; Zehentner, 2016). The method is implemented within
the software package Gravity Recovery Object Oriented Programming System (GROOPS)
developed at the IfG. The raw observation approach was �rst used for kinematic orbit
estimation of GRACE and GOCE (Zehentner and Mayer-Gürr, 2014) and later applied to
various satellite mission like CHAMP, Constellation Observing System for Meteorology,
Ionosphere and Climate (COSMIC), C/NOFS, TerraSAR-X, TanDEM-X, Meteorological
Operational satellite programme (MetOp), Swarm, Jason and the Sentinel satellites
(Zehentner, 2016). All of them were used to retrieve static and time variable gravity �eld
information. The approach is based on the concept of directly using all GNSS
observations of any kind in a common least-squares adjustment. Meaning code and
phase observations on all available frequencies are used without forming linear
combinations. Thus in�uences on the observables must be known in advance or set up as
parameter in the estimation. For example the ionospheric in�uence is set up as
slant total electron content parameter for each tracked GNSS satellite in each
epoch. On the one hand this leads to a high number of parameters but on the
other hand gives the possibility to access and analyse each of these parameters
individually. A unique aspect of the kinematic orbit processing at the IfG is the fact that
azimuth and nadir dependent phase and code antenna centre variations are used
routinely for receivers and transmitters. Furthermore an important aspect is a realistic
observation weighting. This is achieved by generating and using azimuth and nadir
dependent accuracy information for each individual receiver by analysing observation
residuals.
Kinematic Baselines produced at TU Delft
The KBs for the Swarm A and C pair of satellites will be computed with the Multiple
satellites Orbit Determination using Kalman �ltering (MODK) tool, which is an add-on tool
of the GHOST software that is developed and maintained by Deutsches Zentrum für Luft-
und Raumfahrt (DLR) German Space Operations Centre (GSOC), with support by the
TU Delft (Montenbruck et al., 2007; Barneveld, 2012).
The MODK relies on an iterative Kalman �ltering procedure, where carrier-phase ambiguities are resolved as much as possible using a reduced-dynamic orbit determination technique. MODK has the capability to derive the KBs after the carrier-phase ambiguity �xing. The MODK tool has been enhanced with the possibility to use frequency dependent antenna correction maps for both carrier-phase and code observations (Mao et al., 2017). For this project, the MODK tool will be extended with the capability to provide covariance information for the KBs.
Kinematic Baselines produced at AIUB
AIUB has gained experience in precise baseline determination from the analysis of data
from the GRACE, TanDEM-X, and Swarm missions using di�erential GPS with ambiguity
�xing (Jäggi et al., 2007; Jäggi et al., 2012; Jäggi et al., 2016). Precise baseline determination
from Swarm is challenged by ionospheric disturbances and half-cycle ambiguities which
are present in the GPS data. Whereas the impact of the ionospheric disturbances could be
reduced thanks to several updates performed in the tracking loop settings (Dahle, Arnold
and Jäggi, 2017), the latter could recently by circumvented as described by (Allende-Alba
et al., 2017). The AIUB is thus in an excellent position to exploit precise Swarm baselines
also for gravity �eld recovery. First gravity �eld recovery experiments using real
data from GPS-based precise GRACE baselines were already performed by Jäggi
et al. (2009), who showed in particular that a gain of about a factor of ten in the
accuracy of the space baseline (using di�erential GPS with ambiguity resolution
techniques) with respect to the corresponding precise point positioning results is
not accompanied by a corresponding gain (of the same factor of ten) in gravity
�eld determination. This at �rst sight puzzling result is caused by the fact that
di�erential GPS with ambiguity resolution substantially reduces (actually by this
factor of ten) the errors of long period (10-20 minutes) in the baseline, but not the
noise of subsequent position di�erences. Simulations related to Swarm gravity
�eld recovery are often based on the above mentioned seemingly plausible, but
erroneous assumptions concerning noise reduction (e.g., Wang, Gerlach and Rummel
(2012)). Nevertheless, Jäggi et al. (2009) also concluded that the use of GPS-derived
inter-satellite kinematic baselines is worth to be further studied for gravity �eld
determination because of the possible reduction of systematic errors in the GPS
results by forming observation di�erences. Better tools are meanwhile available at
AIUB for GRACE K-Band data analysis and will be adapted in the frame of this
project to exploit Swarm precise baseline solutions for gravity �eld recovery by
treating GPS-derived inter-satellite vectors in close analogy to GRACE K-Band
measurements.
The individual solutions are produced independently by di�erent institutes, following the choices, assumptions and input KOs established by the corresponding responsible scientist. It may be the case that (e.g.) a particular type of KO produces much better gravity �eld models in one gravity �eld inversion approach but that is not the case in a di�erent approach. The same can be said about empirical accelerations, decorrelation strategies, etc. This variety in approaches, assumptions and input data considered in the production of individual solutions is what confers robustness to the combined model and is the strongest asset in our proposal.
| Inst. | Location | Approach | Reference |
| Bern, Switzerland | Celestial Mechanics Approach | Jäggi et al. (2016) |
|
| Prague, Czech Rep. | Decorrelated Acceleration Approach | Bezděk et al. (2016) |
|
| Graz, Austria | Short-Arcs Approach | Zehentner and Mayer-Gürr (2016) |
|
| Columbus, USA | Energy Balance Approach | Guo et al. (2015) |
|
The next sections brie�y describe the 4 gravity �eld determination approaches considered in the production of the individual gravity �eld models.
The Celestial Mechanics Approach
The variational equations approach (Reigber, 1989), of which the Celestial Mechanics
Approach (CMA) (Beutler et al. 2010) is a variant of, connects the measured distances from
the GPS satellites (or other GNSS measurements, SLR observations, KO data or ll-SST
tracking data) and a set of unknown parameters which may include Stokes coe�cients,
initial state vectors, empirical accelerations, drag coe�cients, instrument calibration
parameters (e.g. accelerometer) and other parameters which play a role in the
dynamic equations of motion of the satellite. This is accomplished by linearising the
mathematical model describing the motion of the satellite when considering a
priori reference gravity �eld model and remaining a priori assumptions (such
analytically-derived initial state vectors, initial guess for drag coe�cients, calibration
parameters provided by instruments manufacturer, etc.). The linearisation is performed
(usually numerically) around the reference model response, i.e. the values of the unknown
parameters computed from the reference model when considering the a priori
assumptions.
The CMA is exploited by Astronomical Institute of the University of Bern (AIUB).
The Decorrelated Acceleration Approach
The so-called acceleration approach exploits Newton's equation of motion directly
(Rummel, 1979) and is the foundation for the Decorrelated Acceleration Approach (DAA)
(Bezděk et al. 2014; Bezděk et al. 2016). The method connects the double-di�erentiated
orbital positions to the external forces acting on the satellite. This approach i) avoids
numerical integration operations characteristic of other approaches, and ii) computes the
geopotential harmonic coe�cients from a linear (not linearised) system of equations. The
observations are �rst transformed to the inertial reference frame before di�erentiation to
avoid the computation of �ctitious accelerations. The di�erentiation of noisy observations
leads to the ampli�cation of the high-frequency noise. However, it is possible to handle the
high-frequency noise with a decorrelation procedure, so far for this purpose a �tted
autoregressive process has been used.
The DAA method has been developed by the ASU and applied successfully to Swarm kinematic orbits to produce the monthly gravity �elds (Bezděk et al., 2016).
The Short-Arcs Approach
The short arc integral approach is described in detail by Mayer-Gürr (2006). It has been
used to generate several global gravity �eld models based on CHAMP and GRACE data,
namely the ITG-GRACE (Mayer-Gürr, 2007; Mayer-guerr et al., 2010), the ITG-CHAMP (Ilk,
Mayer-Gürr and Feuchtinger, 2004) models as well as the latest models ITSG-GRACE2014
(Mayer-Gürr et al. 2014) and ITSG-GRACE2016 (Klinger2016). The method is
based on the solution of the Newton's equation of motion by double-integration
and formulation as a boundary value problem. The unknown boundary values
(start and end position of each arc) are estimated in a least-squares adjustment
along with additional parameters which may include the Stokes coe�cients and
empirical parameters for non-conservative forces or calibration parameters, like
accelerometer biases or drifts. As observations hl-SST data as well as ll-SST data may be
included. The name short arc refers to the fact that observation data is usually
split into arcs with a length of 20 to 60 minutes. The normal equations are set up
for each arc individually and later combined on the level of normal equations.
Variance component estimation is used to de�ne the relative weighting between the
arcs.
The Short-Arcs Approach (SAA) is used at Institute of Geodesy Graz (IfG) to produce gravity �eld models.
The Energy Balance Approach
The Energy Balance Approach (EBA), also known as energy integral approach, is based on
the energy conservation principle (O'Keefe, 1957; Jekeli, 1999; Gerlach, 2003; Gerlach et al.,
2003). This principle states that the variations in kinetic energy of the satellite are equal to
the work done by the all forces directed parallel to the velocity vector. Conservative forces,
such as gravitational accelerations, can be related to their potential, providing a linear
relationship to the unknown spherical harmonics coe�cients. The formulation and
applications of earlier EBA methods developed for CHAMP and GRACE gravity �eld
inversion include Han et al. (2005) and Han, Shum and Jekeli (2006). An improved EBA
formulation enabled a 4 order of magnitude improvement in precision of the GRACE KBR
data-derived disturbance potential observables (Zeng2015a; Guo et al., 2015; Shang et al.,
2015), as compared to prior studies, e.g., Jekeli (1999). The derived disturbance potential
observables, when used in temporal gravity �eld inversion have achieved similar level of
accuracy as the o�cial GRACE L2 products Shang et al. (2015). We will revise
the EBA formulation here for Swarm temporal gravity �eld estimation for this
project.
The EBA is exploited by Ohio State University (OSU).
The quality assurance of all intermediate products is solely the responsibility of the scientist responsible for the corresponding WP, see 3.2. He/she will be responsible for conducting internally-de�ned measures and veri�cation procedure to be sure that the data is of the highest quality, stored in in the de�ned format and uploaded error-free to the exchange server.
In what regards the data to be disseminated to Payload Data Ground Segment (PDGS), WP300 (Swarm models validation) will ensure that the combined models have the expected residuals relative to GRACE and, in those months when GRACE models are not available, they describe basin-wide mass variations with the expected magnitude and with a valid geophysical meaning. This veri�cation will be documented in TN-03 (deliverable to WP300).
In its most basic form, the validation quanti�es in aggregate statistics, such as RMS, the geoid height di�erences relative to GRACE, at those wavelengths that Swarm is sensitive to. On example of this quanti�cation is shown in 1.
In the SoW, no requirements were de�ned regarding the quality of the Swarm gravity �eld models. We will however assess and demonstrate the quality of the products in several ways, namely those used by Teixeira da Encarnação et al. (2016), Figures 1-10 and Table 3.
This section gives some details on the proposed implementation strategy. Due to the particularly limited funding in comparison to the size of the project team and the number of institutes involved, the project is designed to be carried out as much independently as possible. 4.3.1 and 4.3.3 describe additional details regarding this set-up.
The WPs are intended to be exclusively assigned to one particular sub-contractor, in order to minimize the management burden during the project activities. It is intended that from the Kick O� (K/O) date, all partners are fully aware of their tasks, so that their e�orts are directed towards processing data and the analysis required in Tasks 2, 3 and 5 of the SoW. In this way, the work can be carried out independently, only being assembled together at a later stage and within a parent WP1 given the inputs from sub-WPs2 . Evidently, the independence of the work in WPs does not preclude the necessary management activities and progress monitoring, at the discretion of the parent WP leader, institute team leader of project leader (more on this in 4.3.1 and 4.6).
In setting up the project in this streamlined fashion, we intend to reduce the workload of all partners and, as a consequence, reduce the costs in order to maximize the time dedicated to the project activities. Additionally, the largest share of management e�orts is put in this document, so that there is minimal need to spend time in those activities during the project execution. The disadvantage of this set-up is that there are numerous WPs, but given the numerous partners and intermediate products, that would probably be the case in any other WP arrangement.
3 lists the WPs and the time devoted by each partner.
| Reference | Name | TU Delft | AIUB | ASU | IfG | OSU |
| WP100 | Documentation of the Swarm Gravity Field Processors | 20 | 0 | 0 | 0 | 0 |
| WP200 | Swarm data pre-processing, KBs and accelerometer data | 0 | 0 | 264 | 0 | 0 |
| WP210 | GPS data pre-processing algorithms | 0 | 40 | 0 | 0 | 0 |
| WP220 | Trade-o� between Swarm accelerometer data and non-gravitational models | 0 | 0 | 200 | 0 | 0 |
| WP221 | Modelled non-gravitational accelerations (ASU) | 0 | 0 | 200 | 0 | 0 |
| WP222 | Modelled non-gravitational accelerations (TU Delft) | 20 | 0 | 0 | 0 | 0 |
| WP223 | Measured non-gravitational accelerations | 0 | 0 | 200 | 0 | 0 |
| WP230 | KBs for gravity �eld estimation | 0 | 0 | 0 | 20 | 0 |
| WP231 | KBs derived from Swarm GPS data (AIUB) | 0 | 30 | 0 | 0 | 0 |
| WP232 | KBs derived from Swarm GPS data (TU Delft) | 30 | 0 | 0 | 0 | 0 |
| WP300 | Swarm models validation | 40 | 0 | 0 | 0 | 0 |
| WP400 | Swarm models processing | 0 | 0 | 0 | 92 | 0 |
| WP411 | KOs (AIUB) | 0 | 60 | 0 | 0 | 0 |
| WP412 | KOs (IfG) | 0 | 0 | 0 | 80 | 0 |
| WP413 | KOs (TU Delft) | 20 | 0 | 0 | 0 | 0 |
| WP421 | Swarm gravity �elds (AIUB) | 0 | 60 | 0 | 0 | 0 |
| WP422 | Swarm gravity �elds (IfG) | 0 | 0 | 0 | 60 | 0 |
| WP423 | Swarm gravity �elds (ASU) | 0 | 0 | 250 | 0 | 0 |
| WP424 | Swarm gravity �elds (OSU) | 0 | 0 | 0 | 0 | 50 |
| WP430 | Combined Swarm gravity �elds models | 0 | 35 | 0 | 0 | 0 |
| WP440 | Data transfer | 20 | 0 | 0 | 0 | 0 |
| WP450 | User support | 10 | 0 | 0 | 0 | 0 |
| WP500 | Publication and presentation of project results | 48 | 0 | 0 | 0 | 0 |
| - | Total | 208 | 225 | 1114 | 252 | 50 |
The work to be carried out in each WP is described in the following sections. Refer to 2 to better visualise the relation between the WPs. Note that there is no WP410 nor WP420 because the activities allocated to those WPs, i.e. the production of KOs and the individual gravity �eld solutions, respectively, is to be conducted completely independently by the various institutes.
The objective of WP100 is to address Task 1 of the SoW. Given the numerous gravity �eld inversion strategies within the project, the deliverable TN-01 will provide the description of their most important aspects, both common and divergent. This document will brie�y describe the EGSIEM standards, since those are the standards considered in our software (and not GRACE and GRACE-FO standards, as suggested in the SoW), and ensure that all processors are in agreement with those standards.
Additionally, there is no need to adapt the existing processors to the Swarm data (as suggested in the SoW), since all processors are already producing gravity �eld models from those data.
WP200: Swarm data pre-processing, KBs and accelerometer data
The objective of WP200 is to address Task 2 of the SoW. This WP is divided into sub-WPs (see the next sections) representing individual tasks needed in order to produce the deliverable TN-02. The work to be carried out speci�cally in WP200 is to:
The end of this WP marks the Mid-Term Review (MTR), when all partners will agre on type of non-gravitational accelerations to be considered by all gravity �eld processors.
Finally, this WP includes the workload required to manage the progress of the activities
in the sub-WPs.
The objective of WP210 is to address Task 2 of the SoW, speci�cally the items referring to the de�nition and implementation of Swarm GPS data pre-processing procedures and algorithms. To meet this objective, the currently implemented data screening procedures in all KO-producing partners will be documented in the deliverable TN-02.1.
Particular to the Swarm data are the e�ects of the geomagnetic activity, which introduce
artefacts in the gravity �elds, (Arnold et al., 2015; Jäggi et al., 2016; Dahle, Arnold and Jäggi,
2017). This WP will provide guidelines for the best data screening procedure that other
KO-producing partners should follow, possibly in the form of time-indexed masks, for each
Swarm satellite.
The objective of WP220 is to address Task 2 of the SoW, speci�cally the items referring to the non-gravitational accelerations used in the inversion of the gravity �elds. To meet this objective, the DAA (implemented at ASU) will be used to compute 3 types of gravity �elds, each considering:
Therefore, the activities of this WP consist of:
The selection of which months will be analysed is left to the WP manager but should be
su�cient to describe di�erent levels of geomagnetic activity and consider the (expected)
quality of the corresponding GRACE solution.
The objective of WP221 is to produce the non-gravitational accelerations following the model implemented at ASU to be considered in WP220. The work to be carried out in this WP is:
The objective of WP222 is to produce the non-gravitational accelerations following the model implemented at TU Delft to be considered in WP220. The work to be carried out in this WP is:
The objective of WP223 is to prepare the measured non-gravitational accelerations of Swarm-C to be considered in WP220. The work to be carried out in this WP is:
The objective of WP230 is to address Task 2 of the SoW, speci�cally the items referring to the added value of additional ll-SST observations, aka Kinematic Baselines (KBs), used in the inversion of the gravity �elds. The purpose of this analysis is to provide a clear guidelines for future studies and the KB data is not (necessarily) going to be considered in the nominal gravity �eld processing of WP421 to WP424.
The SAA (implemented at IfG) will be used to compute 3 types of gravity �elds, each considering:
Therefore, the activities of this WP are:
The selection of which months will be analysed is left to the WP manager but should be su�cient to describe di�erent levels of geomagnetic activity and consider the (expected) quality of the corresponding GRACE solution.
The objective of WP231 is to produce the KBs following the procedure implemented at AIUB to be considered in WP230. The work to be carried out in this WP is:
The objective of WP232 is to produce the KBs following the procedure implemented at TU Delft to be considered in WP230. The work to be carried out in this WP is:
The objective of WP300 is to address Task 3 of the SoW. The work to be carried out in this WP is:
The selection of which months will be analysed is left to the WP manager but should be su�cient to describe di�erent levels of geomagnetic activity and consider the (expected) quality of the corresponding GRACE solution.
More details on the procedure used to analyse, interpret the di�erence relative to
GRACE is given in 2.4.
The objective of WP400 is to address Task 4 of the SoW. The work to be carried out in
this WP consists of producing the detailed description of products to be published on
Swarm Data Handbook and the gravity �eld models (TN-04, DL-01 respectively).
Additionally, this WP includes the workload required to manage the progress of the
activities in the sub-WPs.
The work to be carried out in this WP is:
The work to be carried out in this WP is:
Note that no KBs are to be produced in this WP.
The work to be carried out in this WP is:
The work to be carried out in this WP is:
The work to be carried out in this WP is:
The work to be carried out in this WP is:
The work to be carried out in this WP is:
The objective of WP430 is to combine the four gravity �eld solutions (DL-01.2.1, DL-01.2.2, DL-01.2.3 and DL-01.2.4). The work to be carried out in this WP consists of:
The objective of WP440 is implement the semi-automated procedure that will disseminate the Swarm gravity �eld models. Also included in this WP is the management of the �le server, through which the data is exchanged between the team members. More speci�cally, this WP consists of:
The objective of WP450 is to address Task 4 of the SoW, speci�cally what concerns the responding to user questions regarding the Swarm gravity �eld models.
The objective of WP500 is to address Task 5 of the SoW. The work to be conducted in this WP is:
As indicated in the SoW, the project duration will be 12 months between the K/O meeting to the �nal milestone (MIL-05). The earliest possible K/O date is proposed to be no sooner than September 2017. 3 illustrates the duration of the WPs and the important milestones.
As indicated in 3, the project is, as suggested in the SoW, divided into a preparatory phase and a production phase. The preparatory phase includes WP100 and WP200 and will address Tasks 1 and 2 in the SoW. Importantly, WP200 (speci�cally WP220) will gather the necessary arguments to suggest the input accelerometer data scenario (see the description of WP220 in 3.2) for the production of the gravity �elds.
The preparatory phase ends with the MTR at MIL-02 (K/O + 6 months). WP300 and WP400 start the production phase, with the former WP dedicated to validating a representative sub-set of combined gravity �eld models and the latter producing said models (but not restricted to those). For this reason, WP300 (Swarm models validation) overlaps with WP430 (Combined Swarm gravity �elds models) for one month. The end of WP300 marks MIL-03 (K/O + 8 months) and the end of WP400 and WP500 (K/O + 12 months) determines MIL-04 and MIL-05, respectively, which coincide in the proposed schedule. Irrespective of MIL-04, the deliverable DL-01 (the combined gravity �eld models) is predicted to start being delivered as early K/O + 8 months (2 months before what is suggested in the SoW).
As it can be seen and in comparison to Section 6.2 of the SoW, the milestones have been adjusted to accommodate the large e�ort devoted to WP200, where 2 di�erent non-gravitational force models (in addition to accelerometer measurements from Swarm-C) and 2 di�erent strategies for estimating KBs will be analysed. This means MIL-02, MIL-03 and MIL-04 are postponed for 2 months. In response to the SC-01 requirement, the consortium justi�es this delay as being the time needed for conducting the studies of WP200 properly and to a high level of quality.
In order to minimize cost, the number of meetings is kept to the absolute minimum and is limited to the K/O and MTR. All meetings are to be conducted remotely, through WebEx, to minimize travel costs and maximize the funding for the numerous institutes. The attendance to the Swarm DQW, where the �nal results are going to be presented (MIL-05), is the only travel foreseen.
The cadence of delivery of the combined gravity �eld models will be based on existing experience (which resulted in e.g. Teixeira da Encarnação et al. (2016)).
Consecutive steps are:
A one-month di�erence is speci�ed for the production of KO solutions (6-10 months after kick-o�) and gravity �eld solutions (7-11 months after kick-o�) allowing one month for completing step (3) after steps (1)+(3).
The study output shall be compliant with the list of deliverable documents as indicated in the SoW, and summarized in 4.
| SoW task | WP Ref. | WP nane | Deadline (K/O+months) | Deliv. |
| 1 | Documentation of the Swarm Gravity Field Processors | 1 | TN-01 |
|
| 2 | Swarm data pre-processing, KBs and accelerometer data | 6 | TN-02 |
|
| 3 | Swarm models validation | 8 | TN-03 |
|
| 4 | Swarm models processing | 12 | TN-04, DL-01 |
|
| 4 | User support | 12 | DL-04 |
|
| 5 | Publication and presentation of project results | 12 | DL-02, DL-03, DL-05 |
|
Note that the milestones are not in agreement with Section 6.2 of the SoW. As explained in 3.3, this is required in order to accommodate the large e�ort devoted to WP200.
The main deliverables of the proposed study are gravity �eld models computed on the basis of hl-SST Swarm data. The methodology needed to achieve this has been extensively studied (c.f. 2.3) and is an established research topic of the team members at AIUB, ASU, IfG and OSU, with demonstrated achievements in that �eld. No particularly novel techniques for kinematic POD, gravity �eld retrieval and non-gravitational accelerations are proposed, further limiting the risk. Furthermore, in the remote case one of the individual solutions is missing, the combined model can still be produced from the remaining individual solutions. Therefore, the risk of failing to reach the main objective of the study is low.
The SoW proposes to include innovative elements in study, in order to best exploit the gravimetric data collected by the Swarm satellites. These innovative elements are: i) the analysis of the impact of three independent non-gravitational acceleration data sources (WP220) and ii) gravity �eld estimation on the basis of KBs (WP230). Additionally, our proposal further innovates with the production of proper error estimation at the level of the combined gravity �eld model.
To all these innovations is associated the risk that their respective inclusion in the gravity �eld estimation does not bring signi�cant bene�ts. Although this would be a negative result, it still provides useful information regarding the processing of gravimetric hl-SST data and, more importantly, is not a critical factor in the production of the �nal gravity �eld models.
Regarding the risk assessment of the data availability, the project team does not foresee any di�culties in having access to the required Swarm and GRACE data. The numerous external auxiliary products required to successfully complete the objectives of all WPs are publicly accessible, warranting no expected di�culty.
The distribution of work amongst the team members is done in such a way that their e�orts are conducted in a modular fashion, only interfacing with other WPs through the input/output items described in 3.2. This e�ectively means that every team member is independent and free to use the tools that he/she is most comfortable and pro�cient with. Measures have been taken to mitigate the absence of key personnel due to unforeseeable circumstances. In case of TU Delft, ASU and OSU, this is done by including redundant personnel in the team, namely Elisabetta Ior�da, Jaroslav Klokočník and Junyi Guo, respectively. In case of all institutes, the responsibilities of WP managers can easily be (temporarily of permanently) shifted to another team members (in the same institute) in case of need, with no further impact on the progress of the project, given the overlapping expertise of most team members.
The project, as de�ned in the SoW, contains an extensive list of required deliverables (cf. 3.4) that provide the means through which the e�orts conducted in the context of the project are well documented. This level of documentation, in combination with redundancy in the expertise and experience of the team members, and the availability of margins in the time planning, ensures a very low risk of the project not being completed in the allocated time due to unforeseen circumstances concerning availability of key personnel.
This section provides some details regarding the overall expertise of the various institutes
participating in the consortium. Detailed CVs of the individual team members are provided
in
Within the Delft University of Technology (TU Delft), the Astrodynamics and Space missions (AS) research group will be leading the activities describe din this proposal. This group is part of the faculty of Aerospace Engineering at TU Delft. The group addresses technical-scienti�c challenges and opportunities of mapping Earth using space-based, ground-based and airborne observing systems through advancements in measurement system technology, mathematical and physical modelling, and integrated monitoring systems. The integrated research program ranges therefore from theory development, data acquisition, modelling, data processing and validation to interpretation and data distribution. The program includes space system engineering activities related to the development of integrated micro-instruments for Earth observation, design and feasibility studies for future Earth-observing missions as well as scienti�c support to industry and space agencies. Support activities in each �eld include the organization and execution of measurement campaigns and the establishment and maintenance of a geometric research infrastructure.
AS has a long, multi-decadal, experience in the modelling of satellite dynamics and the computation of satellite orbits. Extensive expertise and processing capabilities have been built up for all relevant space-borne techniques, such as SLR, Doppler Orbit Determination and Radio-positioning Integrated on Satellite (DORIS), GPS and Tracking and Data Relay Satellite System (TDRSS) Satellite-to-Satellite tracking (SST), ll-SST, accelerometry, and for Satellite Gravity Gradient (SGG) observations. Data have been processed and analysed for a multitude of satellites including, but not limited to, CHAMP,GRACE, GOCE, LAser GEOdynamics Satellite (LAGEOS) 1 and 2, ERS-1 1 and Second European Remote Sensing satellite (ERS-2), TOPEX/Poseidon (TOPEX/Poseidon), Jason-1, Satellite Pour l'Observation de la Terre (SPOT) 2, ENVIronmental SATellite (ENVISAT) and Swarm. Moreover, TU Delft participated in the ESA GOCE HPF and is currently partner in the Swarm Expert Science Laboratories (Swarm-ESL) that is doing part of the data processing for the ESA Swarm mission.
In addition to processing real data, a comprehensive system has been implemented for simulations of gravity �eld retrieval from the space-borne observation techniques mentioned above for di�erent mission scenarios. AS has participated � and is currently still participating � in several studies to an ESA Next Generation Gravity Mission. Members of AS are formally involved in many relevant international platforms and advisory groups, including several ESA science and mission advisory groups, sections of the International Association of Geodesy (IAG), the EGU, etc.
The proposed activities will greatly bene�t from the cooperation of the expert team
comprising additionally by the Astronomical Institute of the University of Bern (AIUB),
Astronomical Institute Ond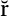 ejov (ASU), Institute of Geodesy Graz (IfG) and Ohio State
University (OSU).
ejov (ASU), Institute of Geodesy Graz (IfG) and Ohio State
University (OSU).
AIUB has a long tradition and strong standing within the International GNSS Service (IGS).
Operational GNSS orbit and clock determination and related research are among the
core activities performed in the frame of the Centre for Orbit Determination in
Europe (CODE), one of the global analysis centres of the IGS. Based on the CODE
products, maximum consistency is achieved for precise orbit determination of LEO by
using the same version of the
Astronomical Institute Ond ejov (ASU) of the Czech Academy of Sciences (AVCR) is the
foremost astronomy organization and one of the oldest scienti�c institutions in the country
(since 1722). The research conducted there is dedicated to a wide range of actual
topics in astronomy, astrophysics and related sciences (from planetary science
to galaxy and black holes studies). Following its long history nowadays the ASU
emerges as a modern public research organization which is involved in a rich set of
international projects in Europe and worldwide. On the national level, the Institute
carries out the major part of research in astronomy and astrophysics in the Czech
Republic. During the recent two decades, the international collaboration of the
Institute has been greatly expanded and it currently represents a signi�cant part of
its research activities, including a close cooperation with European Southern
Observatory (ESO), ESA, International Astronomical Union (IAU) and other professional
organizations.
ejov (ASU) of the Czech Academy of Sciences (AVCR) is the
foremost astronomy organization and one of the oldest scienti�c institutions in the country
(since 1722). The research conducted there is dedicated to a wide range of actual
topics in astronomy, astrophysics and related sciences (from planetary science
to galaxy and black holes studies). Following its long history nowadays the ASU
emerges as a modern public research organization which is involved in a rich set of
international projects in Europe and worldwide. On the national level, the Institute
carries out the major part of research in astronomy and astrophysics in the Czech
Republic. During the recent two decades, the international collaboration of the
Institute has been greatly expanded and it currently represents a signi�cant part of
its research activities, including a close cooperation with European Southern
Observatory (ESO), ESA, International Astronomical Union (IAU) and other professional
organizations.
The ASU team members participating in the project come from the Planetary systems work group of the Galaxies and Planetary Systems department. This work group focuses on the fundamental spatial parameters of the Earth (rotation, Earth's orientation in space), Earth's gravity �eld, celestial mechanics as well as on archeoastronomy. In each category, the group participates in national and international research projects, e.g. ESA-Programme for European Cooperating States (PECS) project on processing GOCE data (2007�2012). Currently we are involved in Cal/Val activities for the Swarm satellite mission, especially on accelerometer-related issues. This comes from the fact that the �rst development phase of space accelerometers aboard Swarm satellites took place at ASU, later the development of accelerometers was fully transferred to Aeronautical Research and Test Institute (VZLU). Members of our group actively participate in international associations and various advisory boards such as IAU, International Earth Rotation Service (IERS) and the IAG (a.o.) and act at universities in the Czech Republic as regular lecturers. The group of Planetary systems is su�ciently equipped with software and hardware resources for solving demanding numerical tasks.
The working group Theoretical Geodesy and Satellite Geodesy is led by Univ.-Prof. Dr.-Ing. Torsten Mayer-Gürr. Since 2015 it is part of the Institute of Geodesy Graz (IfG) headed by Univ.-Prof. Dr. Mathias Schardt, which is part of the Graz University of Technology (TUG). The working group emerged from the former Institute of Theoretical Geodesy and Satellite Geodesy (ITSG). Main topics in research and teaching are analytical and numerical techniques with special attention to satellite geodesy and theoretical geodesy, with a strong focus on global satellite gravity �eld processing. Due to many Earth gravity �eld modelling projects, the working group is able to o�er sustainable experience concerning satellite data processing, time series analysis, solution of large equation systems and gravity �eld model evaluation.
The working group routinely processes GRACE gravity �eld solutions, with the latest release being ITSG-GRACE2016. The group's GOCE and GRACE expertise led to the involvement in various projects, for example the computation of the Gravity Observation COmbination (GOCO) multi-satellite gravity �eld combinations through an international consortium of scienti�c institutions. The working group also contributes to ESA's Climate Change Initiative by providing the GRACE data sets for the Greenland and Antarctica mass balance product. Within the Horizon 2020 funded EGSIEM project, the working group is responsible for establishing a near real-time gravity �eld service which aims at improving �ood and drought prediction using GRACE data. Furthermore, the working group processed the o�cial GOCE-TIM gravity �eld solutions in the frame of the EGG-C, which consists of ten European institutions and universities working under an ESA contract. This experience is also based on more than a decade of pre-mission studies and simulations for GOCE. The accumulated know-how of GOCE-TIM, ITSG-GRACE and GOCO solutions has been combined within the in-house developed software GROOPS, initially developed at the University of Bonn.
The Division of Geodetic Science, School of Earth Science (SES) at The Ohio State University (OSU), Columbus, Ohio, USA, has a substantial heritage in Earth's gravity �eld modelling. Our research group exploits various geodetic measurements including radar/laser altimetry, GNSS, airborne/space-borne gravimetry and gradiometry, Synthetic Aperture Radar (SAR)/Interferometric Synthetic Aperture Radar (InSAR), radiometers, multi-spectral and optical imagery to conduct interdisciplinary Earth science research and applications. Relevant software systems for gravity �eld inversion, orbit determination, and satellite data processing exist and will be available for the project. Existing computing systems3 will be used for computational and �le-serving for the project at no-cost to the sponsor. The Geodetic Science research group at OSU has considerable experience in conducting Earth science research using data from geodetic satellites and has expertise in gravity �eld inversion and precision orbit determination.
The Project Manager is Pieter Visser, who has participated in a number of ESA projects, namely as Co-investigator of many ESA sponsored studies for European gravity �eld missions (ARISTOTELES, GEM, GOCE), Co-investigator Swarm End-to-End Mission Performance Simulator and Work package manager GOCE High-level Processing Facility, amongst others. The TU Delft team also includes i) João Encarnação who will support project management activities, including promotion, consolidation, data documentation, data management and data transfer; ii) Jose van der IJssel who is responsible for providing high-quality KOs and accurate GPS-driven baselines, iii) Eelco Doornbos who will be dedicated to computing the measured and modelled accelerations, as well as their validation and iv) Xinyuan Mao who will assist the computation of baseline solutions.
The TU Delft team is completed with Elisabetta Ior�da. She will support the management tasks by João Encarnação and will be able to take over João's tasks if so required. All team members have a long history of involvement in POD and gravimetric missions, as attested in their CVs.
João Encarnação is not employed by TU Delft and in fact has a guest researcher status. The latter means he has full access to the relevant hardware and software infrastructure of TU Delft and can carry out the foreseen tasks. At Center for Space Research (CSR), he has been granted the liberty to spend the time needed for this project. However, it is not guaranteed that João Encarnação will be employed by CSR for the full duration of this project. Therefore, as mentioned in 3.5, tasks can to be redistributed and other team members will be assigned a heavier task for this project. For TU Delft, we reiterate that this will be Elisabetta Ior�da, currently responsible for part of the TU Delft Swarm-ESL operations and maintenance.
The AIUB team is led by Adrian Jäggi, the director of the AIUB, with the overall responsibility for the activities of the institute. Beside of the contribution in management he can give signi�cant input for scienti�c questions and for technology, in particular for LEO POD and precise baseline determination where he has a long-time experience. The facilities of the EGSIEM project, of which s the PI, will provide substantial support in the activity of merging the various gravity �eld solutions. Daniel Arnold will provide high-quality KOs and GPS-driven baselines, using di�erent software package than TU Delft. Ulrich Meyer's main responsibility is to produce the gravity �eld models, considering the CMA. All team members are actively engaged in world-leading satellite gravimetric and POD research.
At ASU, the expertise of the team leader Aleš Bezděk relevant to this proposal includes the development and implementation of the Decorrelated Acceleration Approach (DAA) (Bezděk et al. 2014; Bezděk et al. 2016) to reduce KOs of LEO satellites to monthly models of Earth's gravity �eld. Additionally, Aleš Bezděk is an active member of the Swarm Cal/Val community, with numerous contributions in Swarm Science meetings and DQWs. Jaroslav Klokočník's background and research expertise are related to space geodesy and geophysical applications of geodetic data, as attested by the numerous publications he has authored, and will provide support in the project activities.
The IfG team is lead by Torsten Mayer-Gürr, who developed the Short-Arcs Approach (SAA) (Mayer-Gürr 2006) that has been extensively used to produce high-quality gravity �eld models, both static and temporal. The team is further comprised of Norbert Zehentner, who is responsible for the production of KOs using in-house software and the production of the monthly models. Finally, Matthias Ellmer will provide overall support to the activities at IfG. The team is further engaged in the EGSIEM project and routinely published important research results in satellite gravimetry.
The �nal team comes from the OSU and is led by C.K. Shum, who has extensive expertise in
satellite geodesy, sea-level studies, satellite oceanography and hydrology, amongst others.
The team from OSU, in particular Junyi Guo, and others have developed an improved
formulation and the associated temporal gravity �eld inversion methodology of the EBA
(
This team is led by C.K. Shum and Junyi Guo, who will provide support to the role of OSU.
The table below lists the institute team leaders:
| Inst. | Leader |
| Pieter Visser |
|
| Adrian Jäggi |
|
| Aleš Bezděk |
|
| Torsten Mayer-Gürr |
|
| C.K. Shum |
|
We propose to distribute work in self-contained WPs, which can be concluded as independently as possible. This approach aims to maximize the e�ort devoted to scienti�c and operational activities in view of limited funding and short study duration.
The modular set-up of the WPs aims to assign all management tasks of that WP to the respective manager. This includes the production of all required documentation and the delegation of tasks within his/her organization, without the explicit need to inform the prime contractor.
A common management procedure in all WPs, to which all project personnel has explicitly agreed with, is that the WP leader is ultimately responsible for the production of the respective deliverable in a timely fashion and in compliance with the WP description and objectives. Therefore, the numbering of the WPs does not re�ect any sort of hierarchy regarding accountability between WPs leaders, but is related to the Tasks described in the SoW. Independently of this, any parent WP manager may request a progress report in order to better coordinate activities of their WP.
The table below lists the WP leaders and the WP(s) they are responsible for:
| WP leader | WP(s) |
| João Encarnação | |
| Aleš Bezděk | |
| Daniel Arnold | |
| Eelco Doornbos | |
| Norbert Zehentner | |
| Adrian Jäggi | |
| Xinyuan Mao | |
| Torsten Mayer-Gürr | |
| Matthias Ellmer | |
| Jose van der IJssel | |
| Ulrich Meyer | |
| C.K. Shum | |
| Pieter Visser | |
Within the proposed activities, the added workload needed to routinely produce KBs by either AIUB or TU Delft (responsible for WP231 and WP232, respectively) cannot be guaranteed given the limited funding and short duration of the activities. More importantly, superior KBs solutions that include attitude information are being developed at AIUB, which may out-perform the scalar KB solution (considered in the proposed activities). As a result, WP421 to WP424 are not (necessarily) going to consider the data produced in WP230, nor are (necessarily) KBs going to be computed outside of the context of that WP.
Each individual solution is produced independently, following the procedures implemented in di�erent institutes and according to the assumptions and trade-o�s that each responsible scientist has chosen. The goal of the proposed project is not to change the autonomous procedure within each gravity �eld-producing institute but to bring the best that their solutions have to o�er to the wider scienti�c community, trough the rigorous combination of the individual solutions.
The consortium agrees that imposing constraints on input data4 , processing algorithms, data screening procedures, parametrization schemes, empirical parameters, etc. would be disadvantageous in the sense it would corrupt and undermine the diversity and robustness of the proposed multi-approach method. As such, it is the responsibility of AIUB, ASU, IfG and OSU to produce gravity �eld solutions according to their own choices regarding (but not limited to) the items listed above, in order to produce the best results according to their internal metrics. This is a self-reinforcing set-up, since every institute is naturally motivated to provide the best possible individual gravity �eld solutions. In view of the limited funding, furthermore, there is no room for an exhaustive study of which KO solutions is the best one for every approach.
The results of the studies conducted in WP200 are guidelines to the gravity �eld processors of those institutes and they may adapt those recommendations in case that improves the quality of their gravity �eld solutions. The motivation for this loose constraint on input data and algorithm speci�cations emerges from the understanding common to all partners that every gravity �eld processor is unique, diverse and better suited to produce higher quality solutions under tested-and-tried conditions. Imposing an exceedingly di�erent set-up to those processors would be risky, time-consuming and would likely bring little or no bene�t to individual solutions, and much less to the combined solution. One important exception to this guideline concerns the EGSIEM standards, which are common to all KO, KB, accelerometer and gravity �eld processors.
An overview of the key personnel for the project is provided below, their role, total number of hours allocated to the project and percentage of total working time dedicated to project activities (considering a total man-hours per year equal to 1670) is presented.
| | | | |
| | | | |
| | | | |
| | | |
|
| | | | |
| | | |
|
| | | |
|
| | | |
|
| | | | |
| | | |
|
| | | |
|
| | | | |
| | | | |
| | | | |
Details on the expertise and experience of the team members is provided in the CVs in
Refer to 3.3.
In order to ensure the deliverables are ready in a timely fashion, the responsibility for every WP is superseded by i) the respective institute team leader (see 4.2) and ii) by the project leader (Pieter Visser). These de-facto leaders are entitled to request a report from any WP leader at their discretion in order to evaluate the progress of the work. These progress reports are necessary to meet the requirements PR-01, ME-02 and ME-04 of the SoW. Additionally, as mentioned in 4.3.1, the WP leader of a parent WP may inquire about the progress of any sub-WP that produces results needed to meet the objective of his/her WP. All WP leaders have explicitly agreed to promptly respond to any such request, addressing all inquires in the most accurate way possible.
The project activities start immediately after the K/O meeting, according to the schedule illustrated in 3. In response to the PR-01 requirement given in the SoW, the project leader shall describe the progress of the project in a short monthly email report. In response to the ME-02 requirement given in the SoW, the project leader shall contact the Swarm DISC project o�ce via WebEx every two months. The MTR shall take place via WebEx and all institute team leaders shall be present, as well as any team members if they so require. In response to the ME-03 requirement given in the SoW, the project leader shall prepare and deliver a presentation of the main project results or delegate this task to another project team member.
Minutes of meetings shall be taken by the project manager, or by a person duly appointed by him. Minutes shall be distributed to the required recipients within 2 working days of the meeting. Bi-monthly progress reports shall be made available and will contain all the necessary information in compliance with the requirements of the contract.
The bidder states compliance to all the requirements stated in the SoW with the exception of the entries in the table below, where an adjustment is proposed or a clari�cation is given in italic font.
| Requirement | Comment |
| MG-01 | The project manager is Pieter Visser. |
| MG-02 | The subcontractor points of contact are given in the cover letter to this proposal. |
| MM-01 | [...] send |
| DL-01 | Time series of |
| DL-02 | One Peer reviewed publication submitted |
| DL-03 | Presentation of project achievements to Swarm DQW,
|
| DL-04 | E-mail replies to 2 |
For the activities proposed to be performed in the context of the current proposal, the project team does not intend to use any background intellectual property not owned by the participating institutes and is, therefore, not required to pay any related fees.
Regarding intellectual property owned by the participating institutes, it is understood that the software packages used within this project is under continuous scienti�c development. No development of the software packages will be carried out in the frame of this project. All intellectual property rights over the software listed in 7 will stay with the respective institutes.
In response to the third paragraph of Section 5.7.2 of the Special Conditions of Tender (SCoT), the software listed in 7 is needed for the production of (part of) the deliverables but is not needed subsequent to the delivery. There is, therefore, no need to establish the conditions of access of ESA/DISC to the listed software, which remains at the discretion of the respective institutes.
| | |
| |
|
| |
|
| |
|
| |
|
| |
|
Allende-Alba, Gerardo et al. (2017).
Arnold, D. et al. (2015).
Balmino, G. et al. (1999).
Barlier, François (2005).
Barneveld, Pieter Willem Lucas van
(2012).
Beutler, Gerhard et al. (2010).
Bezděk, A, J Sebera and J Klokočník (2014).
Bezděk, Aleš (2010).
Bezděk, Aleš et al. (2009).
Bezděk, Aleš et al. (2014).
Bezděk, Aleš et al. (2016).
Bock, Heike et al. (2011).
Bock, Heike et al. (2014).
Cohen, Steven C. and David E. Smith (1985).
Combrinck, Ludwig (2010).
Dach, Rolf et al. (2017).
Dahle, C., D. Arnold and A. Jäggi (2017).
Dorrer, M, B Laborde
and P Deschamps (1991).
Duchossois, G. (1991).
Edwards, P. G. and D. Pawlak (2000).
Flechtner, Frank et al. (2014).
Floberghagen, Rune et al. (2011).
Francis, C. R. et al. (1995).
Gallis, Michael A. et al. (2014).
Gerlach, Ch. (2003).
Gerlach, Christian et al. (2003).
Guo, J. Y. et al. (2015).
Han, Shin-Chan Chan, C. K. Shum and
Christopher Jekeli (2006).
Han, Shin-Chan Chan et al. (2005).
Helleputte, T. van (2004).
IJssel, Jose van den, Biagio Forte and Oliver Montenbruck (2016).
IJssel, Jose van den et al. (2015).
Ilk, Karl Heinz, Torsten Mayer-Gürr and Martin Feuchtinger (2004).
Jäggi, A. et al. (2007).
Jäggi, A. et al. (2009).
Jäggi, A. et al. (2012).
Jäggi, A. et al. (2016).
Jäggi, Adrian, U. Hugentobler and G. Beutler (2006).
Jean, Y., U. Meyer and A. Jäggi (2015a).
Jean, Yoomin, Ulrich Meyer and Adrian Jäggi (2015b).
Jekeli, Christopher (1999).
Kuo, U Ying-Hwa, C. Rocken and Richard A. Anthes (2005).
Kuo, Y.H., B. F. Chao and L. C. Lee (1999).
Larkin, Philip (2012).
Mao, X. et al. (2017).
Mayer-guerr, Torsten et al. (2010).
Mayer-Gürr, T (2007).
Mayer-Gürr, T et al. (2014).
Mayer-Gürr, Torsten (2006).
Montenbruck, O et al. (2007).
O'Keefe, John A. (1957).
Picone, J. M. et al. (2002).
Polischuk, Georgy M. and Sergey G. Revnivykh (2004).
Reigber, C, P Schwintzer and H Luehr (1996).
Reigber, Christoph (1989).
Rummel, R. (1979).
Shang, Kun et al. (2015).
Sheard, B. S. et al. (2012).
Smith, David E. and Donald L. Turcotte (1993).
Stewart, R. (1981).
Tapley, B., C. Reigber and W Melbourne (1996).
Tapley, Byron D. et al. (2004).
Teixeira da Encarnação, João et al.
(2016).
Teixeira Encarnação, João et al. (2017).
Wang, Xinxing, Christian Gerlach and Reiner Rummel (2012).
Weigelt, M. et al. (2013).
Wermuth, Martin, Oliver Montenbruck and Tom Van Helleputte (2010).
Willis, Pascal, Christian Jayles and Yoaz Bar-Sever (2006).
Zehentner, Norbert (2016).
Zehentner, Norbert and Torsten Mayer-Gürr (2014).
� (2016).